미분 가능성
$(y-\hat{y})^2$은 미분가능하므로 최적화가 쉽다. 이를 일반적으 설명하기위해 $f(x)=x^2$ 함수를 생각해보자. $f(x)$ 가 미분 가능할 때 $f(x)$를 최소화하는 $x$ 값을 구하는 일반적인 방법중 하나는 뉴턴 방법(Newton's method)이다.
노트: 거칠게 말해 미분이란 그래프로 함수를 그렸을 때 접선의 기울기를 구할 수 있는가이다.
뉴턴 방법은 시작점 $x_1$으로부터 시작해 $f(x)$가 점점 더 작아지게 되는 $x_2, x_3, \cdots$를 반복적으로 구한다. 뉴턴방법이 주어진 $x_n$보다 $f(x)$를 더 작게 만드는 $x_{n+1}$을 구하는 방법은 아래 그림과 같다.
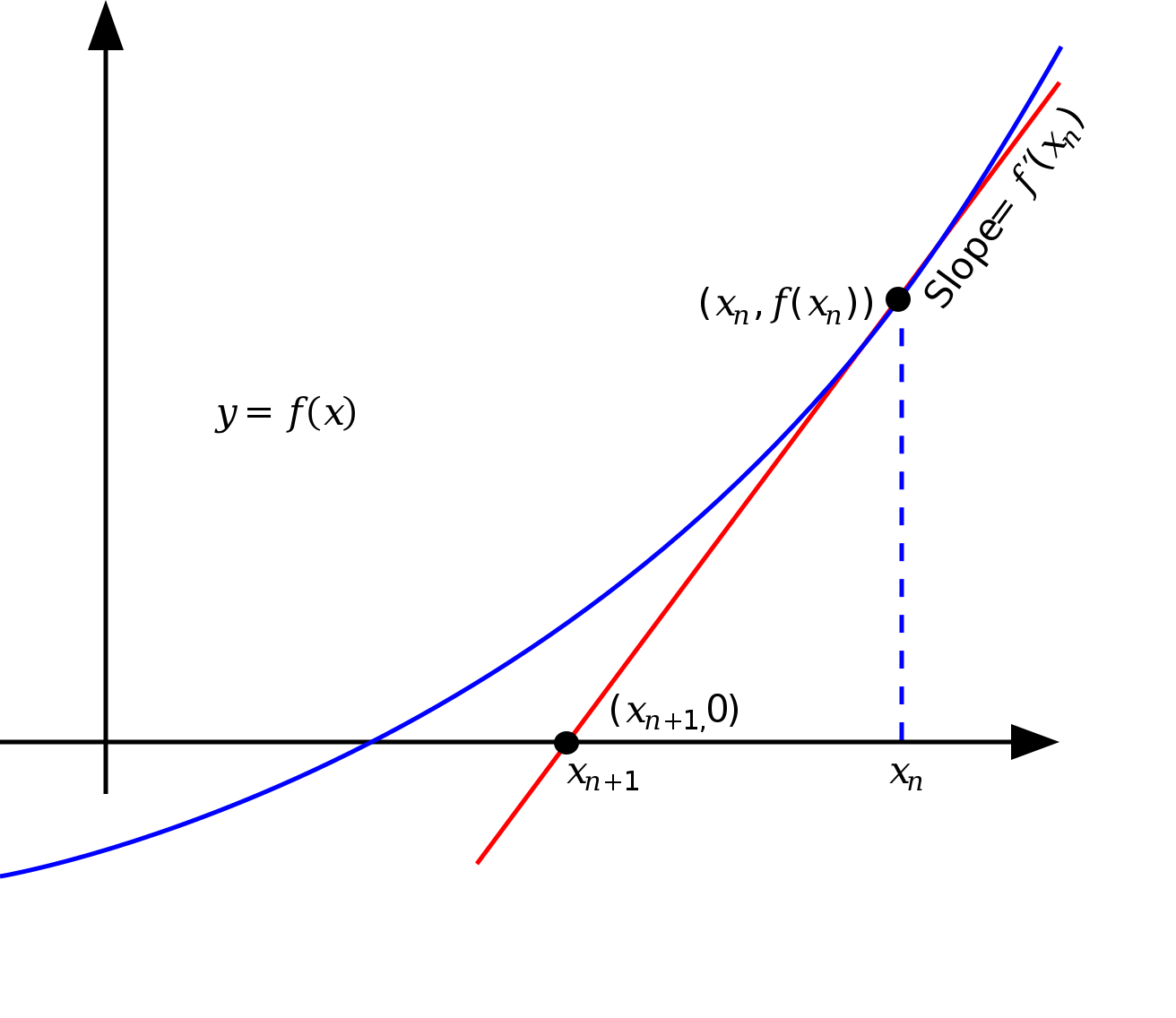
- $x_n$이 현재 출발점이라고 하자.
- $x_n$에서 접선을 긋고, 그 접선이 x 축과 만나는 점을 $x_{n+1}$이라고 하자.
- $f(x_{n+1})$은 $f(x_n)$보다 작은 값이 된다.
2 단계처럼 접선을 그어 x 축과 만나는 $x_{n+1}$을 구하는 방법은 다음과 같다.
\[ x_{n+1} = x_{n} - {{f(x_n)} \over {f'(f_n)}} \]
이처럼 최적화 목표가 미분 가능하면 다양한 방법들을 사용해 그 목표를 최소화 시킬 수 있다.
반면 선형 회귀에서 가장 직관적일 것 같은 최적화 목표인 $|y-\hat{y}|$는 미분 가능하지 않다. 따라서 SSE와 달리 최적화가 더 어렵다.